Kwalifikacja: EE8 - Kwalifikacja EE8
Zawód: Technik informatyk
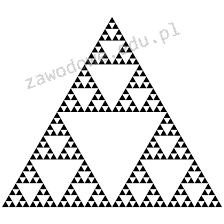
Na rysunku przedstawiono
Odpowiedzi
Informacja zwrotna
W tym rysunku widzimy trójkąt Sierpińskiego, który pokazuje, jak wyglądają obiekty samopodobne. To znaczy, że jak spojrzysz na mniejsze trójkąty w środku, to one wyglądają jak całe. Trójkąty Sierpińskiego są naprawdę ciekawe, bo można je wykorzystać w różnych sprawach, zwłaszcza w grafice komputerowej do tworzenia fajnych obrazków i złożonych wzorów, jak chmury czy góry. Oprócz tego, takie struktury samopodobne pomagają w analizie danych i modelowaniu różnych zjawisk w naturze. Myślę, że zrozumienie tych rzeczy jest ważne, bo matematyka fraktalna robi się coraz bardziej popularna, zwłaszcza w naukach przyrodniczych i inżynierii, gdzie musimy badać skomplikowane systemy w nowy sposób.
Wybierając tę odpowiedź, pewnie poszedłeś w nieco innym kierunku, związaną z fraktalami. Kostka Mengera to inny typ fraktala, który także ma to samopodobieństwo, ale to nie jest to samo co trójkąt Sierpińskiego. Krzywe smocze to znowuż inny przykład, który jest dosyć skomplikowany, ale nie wygląda tak jak trójkąt Sierpińskiego, jeśli chodzi o budowę. Paproć Barnsleya też jest fraktalem, ale to całkiem inna historia, bardziej złożona. Wybierając te opcje, mogłeś skupić się na tym, jak wyglądają te obiekty, ale ważne jest, żeby nie zapominać o samopodobieństwie. Zrozumienie tego, co sprawia, że te obiekty są różne, naprawdę może pomóc w lepszej analizie i interpretacji skomplikowanych struktur, zarówno w matematyce, jak i w naukach przyrodniczych.